By D. Thomakos
Market reversals are the critical junctures that make or break a market timing strategy. Addressing the concept of reversals is an interesting aspect of research because it conforms to ideas of hidden complexity and non-linear dynamics in asset returns. In this post I offer a simplistic, yet effective, approach for addressing market reversals with the "speculative switch". The idea is rather simple: I am after some condition which will alter the direction of my signaling method, here being simple momentum. The method, however, comes not just with the sign of the momentum but also with the speculative switch: this is a parameter whose sign changes based on a performance and direction-of-trade condition. When the condition is in effect then a change of the predicted sign is applied and trading continues along this new direction. As you will read below the condition is based on how the strategy is doing compared to the passive benchmark and the current direction-of-trade at the time of performance evaluation. More details can be found in the Python code in my github repository.
Consider thus the returns of an asset [math] r_{t} [/math] and the corresponding R period momentum based on the average return [math] m_{t-\delta}(R) \doteq R^{-1}\sum_{j=t-R-\delta+1}^{t-\delta}r_{j}[/math], with [math]\delta[/math] being a delay parameter. Let [math]s_{t}\in\left\{-1,1\right\}[/math] denote the switch parameter. Trading occurs under the following condition:
[math] \widehat{r}_{t+1|t}^{switch} \doteq \left[I(s_{t} > 0)-I(s_{t} \leq 0)\right]\cdot sgn\left[m_{t-\delta}(R)\right]r_{t+1} [/math]
that is, the switch alters the direction of the sign of the momentum - and the switch is time-varying. The condition for changing the sign or direction of the switch depends on the total excess return of the strategy over the last 3 periods [math] x_{t} \doteq \prod_{j=t-2}^{t}(\widehat{r}_{j|j-1}^{switch}+1)-\prod_{j=t-2}^{t}(r_{j}+1) [/math] and the current direction of trade:
[math] s_{t+1} = s_{t} \cdot \left\{1 -2 I\left[(x_{t} < 0 \wedge d_{t} > 0) \vee (x_{t} > 0 \wedge d_{t} < 0) \right] \right\} [/math]
where [math] d_{t} [/math] is the sign of the current direction of trade, as determined by the first equation. What the speculative switch does is to revert the sign of the trade when you either loose to the benchmark and insist on a long trade or you win the benchmark and insist on a short trade. Why might this approach work? Well, that's for you to discover by doing your extra homework. I am going to showcase some results with some ETFs and two cryptocurrencies. They all have been used before in my posts so you can compare methods. The data are daily returns from 2022, again for full comparability with previous exercises. I am parametrizing the problem with the rolling windows in the range [math] R \in \left\{3, 22\right\}[/math] and the delays in the range [math] d\in \left\{0, 3\right\}[/math] with one-step increments. Then, for each asset I report the percentage of times that the strategy made positive excess returns across the 80 total combinations and the average return for each delay from this percentage of successful trading. This gives us a broader understanding of the capabilities of the speculative switch approach. Table 1 below has these results.
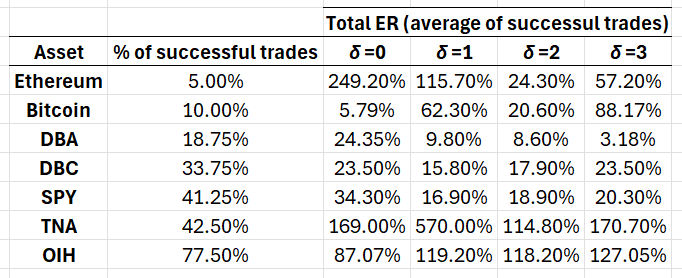
Table 1. Performance attribution of the speculative switch strategy. ER stands for excess returns. Daily rebalancing, data starting in 2022.
The results are eminently interesting. First, it appears that there is (as is always the case) a rolling window and delay combination that will skyrocket performance. Second, the total average return of successful trades is substantial enough (for the period of time in consideration) to justify the appeal of the method. Third, while the cryptocurrencies and commodities have much smaller percentages of successful trades this is not so for the other ETFs, with a percentage of 40% and over - and this is only for my suggestive parametrization, for clearly a more systematic approach would give higher performance benefits. Fourth, and possible more practical from a real-time investing perspective, note that delays of more than two days also generate excellent average excess returns, sometimes being the best delays compared to just using information up to and including the current day.
Don't delay, go grab the Python code and activate your own "speculative switch" - turn it on for profits!
"novus ordo speculationis simplicitatis et parsimonia est".



