By D. Thomakos - with prompts to Gemini
In the complex and often chaotic world of financial markets, the quest for predictable patterns and robust trading strategies is unending. What if we could draw inspiration from a field dedicated to understanding control and communication in dynamic systems? This is precisely the ambitious project we've embarked upon, exploring how the principles of Cybernetics, pioneered by Norbert Wiener, can offer a novel framework for forecasting and trading.
The Cybernetic Lens: Information, Feedback, and Control: Norbert Wiener's Cybernetics fundamentally changed how we think about systems, whether biological, mechanical, or social. At its core, cybernetics is the study of how systems maintain stability and achieve goals through the flow of information and the use of feedback mechanisms. We've applied this lens to financial markets, viewing them as noisy communication channels where valuable signals are often obscured. Key cybernetic concepts at play in our system include:
Information and Entropy: In cybernetics, information quantifies the organization or predictability of a system, inversely related to its entropy (disorder). A market exhibiting high entropy is highly unpredictable, akin to pure noise. Conversely, lower entropy suggests more discernible patterns. We use Sample Entropy (SampEn) to quantify this, where a lower value indicates greater regularity and potential predictability.
Non-linear Forecasting: Financial markets are far from simple linear systems. To capture their intricate dynamics, we employ a non-linear forecasting model based on multiple Wiener integrals, approximated by a Volterra series. This mathematical framework allows us to model complex interactions between past market movements. Our prediction for the next period, [math] \hat{x}_{t+1} [/math], is derived from past returns [math] x_{t-i} [/math] using a series expansion:[math] \hat{x}_{t+1} = K_{0} + \sum{i=0}^{L-1} K_1(i) x_{t-i} + \sum_{i=0}^{L-1} \sum_{j=0}^{L-1} K_2(i, j) x_{t-i} x_{t-j} [/math]. Here, [math]K_{0}[/math] is a constant, [math]K_1(i)[/math] captures linear dependencies, and [math]K_2(i, j)[/math] models quadratic interactions between returns. These [math]K_n[/math] values are our "kernels" – the learned coefficients of our non-linear model.
Adaptive Learning and Feedback Loops: The true power of cybernetics lies in its emphasis on feedback. Our system continuously adapts its forecasting model. When a prediction is made, and the actual market outcome is observed, the error between the two serves as a crucial feedback signal. This error drives the adjustment of our kernels using a gradient descent-like update rule, incorporating L2 regularization to prevent overfitting: [math] K_{new} = K_{old} + \eta \cdot e \cdot \frac{\partial \hat{x}_{predicted}}{\partial K} - \eta \cdot \lambda \cdot K_{old} [/math], where [math]\eta[/math] is the learning rate and [math]\lambda[/math] is the regularization strength. This continuous adaptation allows the system to learn from its past performance, striving for improved accuracy and stability in its predictions.
Building a Cybernetic Trading System: Our work culminates in a Python-based system comprising two main classes: CyberneticTrader and BacktestingEngine. The CyberneticTrader encapsulates the non-linear forecasting model and its adaptive learning mechanism. It processes incoming market data point-by-point, updates its internal "knowledge" (kernels), and generates a forecast for the next period, along with a trading signal (BUY, SELL, or HOLD) based on the forecast's sign. The BacktestingEngine simulates the trading process over historical data, applying the signals generated by the CyberneticTrader. Crucially, it integrates a number of essential risk management features, which you can see in the relevant Python code - the code also includes walk-forward optimization (WFO). Check the code at my github repository (where you can also find more versions of the cybernetic trader!)
Cybernetic Forecasting: To demonstrate the practical application of our Cybernetic Forecaster, we've applied it to a real-world macroeconomic series: the monthly US Inflation Rate (derived from the CPIAUCSL series from FRED). We compare its one-step-ahead forecasting performance against a traditional AR(1) (Autoregressive model of order 1) benchmark. The rolling window evaluation process allows us to see how both models adapt and perform over different economic regimes. Metrics like Mean Squared Error (MSE), Mean Absolute Error (MAE), and Sign Prediction Accuracy are used to quantify performance. While the Cybernetic Forecaster has the potential to capture non-linearities, the AR(1) provides a strong linear baseline for comparison.
Conclusion and Future Directions: Our exploration into cybernetic forecasting and trading has laid a robust foundation for a new paradigm in quantitative finance. By embracing Wiener's principles of information, feedback, and control, we've developed a system that can adaptively learn non-linear patterns in financial data and manage risk effectively.However, this is just the beginning. Future work could involve: (a) Higher-Order Kernels: Exploring the computational feasibility and benefits of implementing higher-order Wiener integral kernels to capture even more complex non-linearities; (b) Advanced Optimization: Integrating more sophisticated optimization algorithms (e.g., Adam, Bayesian optimization) for faster and more efficient kernel learning.
Get the detailed user's manual below as a technical summary and explore on your own the cybernetic speculation promise - the plot below should be bait enough for you to check the Python code(s)!
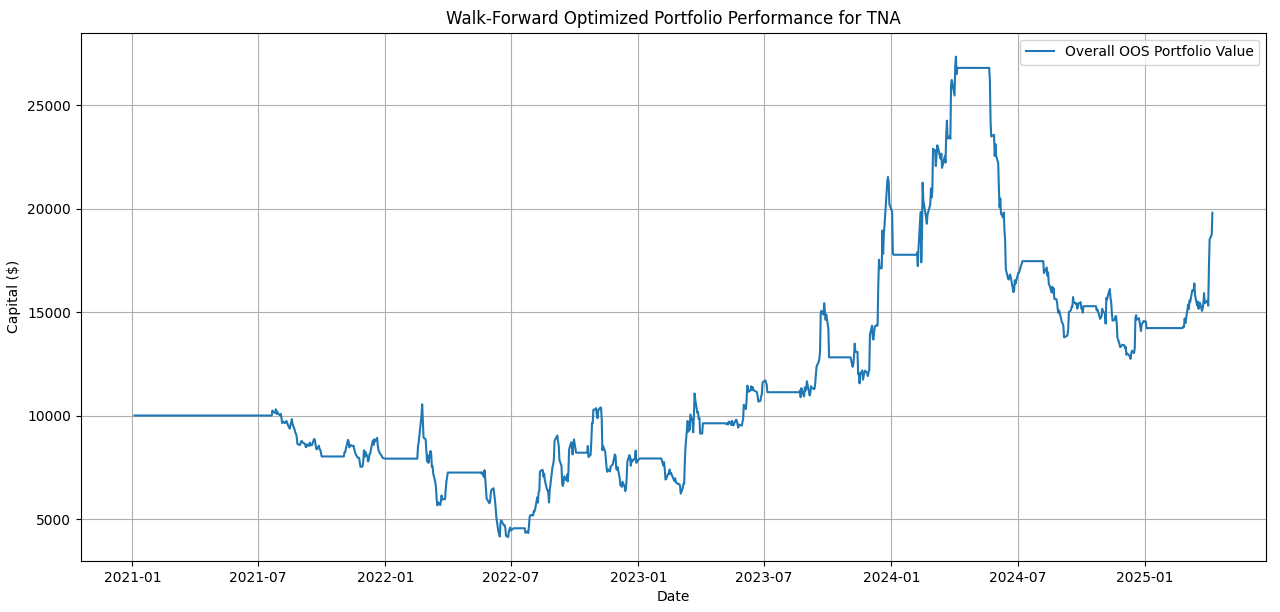
Figure 1. The evolution of NAV for TNA, daily trading, testing and rebalancing every quarter for WFO optimization; total return is 98%.



