By D. Thomakos
The use of learning in quantitative trading strategies is both useful and important. It is useful because it augments our understanding of any trading strategy that issues buy and sell signals; it is important because learning can offer performance enhancements via averaging. In this post I illustrate a novel way to use forecast error learning when performing sign forecasting that is used as input to a trading strategy - and also illustrate averaging via learning. For the case of averaging you can also see this past post and see how the two approaches "blend together". But the particular idea of learning in this post is completely new!
Consider any trading strategy that issues a sign prediction, say [math] \widehat{s}_{t|t-1} \doteq sgn(\widehat{r}_{t|t-1})[/math], about next period's sign [math] s_{t} \doteq sgn(r_{t}) [/math]. Assume that this prediction is obtained using a window of R observations. Then, define the sign forecast error [math] \widehat{e}_{t|t-1} \doteq s_{t} - \widehat{s}_{t|t-1} [/math] that takes three distinct values only [math] \left\{-2, 0, +2 \right\} [/math] (assuming that [math] r_{t} \neq 0 [/math]). Next, consider some other window N of observations, not necessarily the same and usually different from the window used to get the sign forecast, over which you count the number of forecast errors that you make and assign a "loss" of [math] \ell_{t}^{+} \doteq 2^{-n_{t}^{+}}[/math] for the times that you made a positive forecast error (i.e., when the actual sign was positive but your sign forecast was negative) and similarly assign a loss of [math] \ell_{t}^{-} \doteq 2^{-n_{t}^{-}}[/math] for the times that you made a negative forecast error (i.e., when the actual sign was negative and your sign forecast was positive). The total loss due to sign miss-classification is [math] 2^{-n_{t}}[/math]. Here we have that [math] n_{t}^{+} \doteq \sum_{j=t-N+1}^{t}I\left(\widehat{e}_{j|j-1} = 2 \right)[/math] and [math] n_{t}^{-} \doteq \sum_{j=t-N+1}^{t}I\left(\widehat{e}_{j|j-1} = -2 \right)[/math] and [math] n_{t} \doteq n_{t}^{+} + n_{t}^{-}[/math]. The use of base 2 for the computation of the forecast error loss is consistent with the theory of Ray Solomonoff and Jorma Rissanen. In the work of the former the base of 2 weights probabilities across different forecasts for forecast averaging while in the work of the latter the base of 2 is used to suggest a prior distribution for the integers - and the number of times a forecast error is made is an integer.
As time elapses and forecast errors are accumulated we can compute, in addition to the losses [math] \left( \ell_{t}^{+}, \ell_{t}^{-}\right) [/math] the corresponding financial loss from these errors, say [math] h_{t}^{+} \doteq \prod_{j=t-R+1}\left[1+\vert r_{j}\vert I\left(\widehat{e}_{j|j-1}=2\right)\right][/math],and of course similarly for [math] h_{t}^{-}[/math]. The total financial loss is then [math] h_{t} \doteq h_{t}^{+} + h_{t}^{-1} [/math]. Next, define a compositive measure of loss, the ratio [math] \nu_{t}^{+} \doteq \ell_{t}^{+}/h_{t}^{+}[/math], which gets smaller when you either make more miss-classified sign forecasts or when your financial loss increases, and similarly for [math] \nu_{t}^{-}[/math]. Finally, for scaling issues I convert the last measure to [math] w_{t}^{+} \doteq \nu_{t}^{+}/\left(\nu_{t}^{+}+\nu_{t}^{-}\right)[/math] and similarly for [math] w_{t}^{-}[/math].
Armed with all the above I next define my trading strategies that are based on sequential error learning and error weighting, see for example this past post for weighting across different rolling windows. The strategies "learn" from the past sign forecast errors and issue a new forecast based on the sequential losses previously defined. Here we go:
Strategy based on sign loss: define the new signal for period t+1 from the difference [math] sgn\left(\ell_{t}^{+} - \ell_{t}^{-}\right) [/math]. The learning interpretation is straightforward: if your positive forecast errors are more than your negative forecast errors then the signal will be negative, for you have been issuing a lot of false positive signs, and vice versa.</p style="text-align:>
Strategy based on wealth loss: define the new signal for period t+1 from the difference [math] sgn\left(h_{t}^{-} - h_{t}^{+}\right) [/math]. The learning interpretation is also straightforward: if your positive wealth loss is higher than your negative wealth loss then the signal will be negative, for you have been losing money on a lot of false positive signs, and vice versa.</p style="text-align:>
Strategy based on sign and wealth loss: define the new signal for period t+1 from the difference [math] sgn\left(\nu_{t}^{+} - \nu_{t}^{-}\right) [/math] or equivalent from [math] sng\left(w_{t}^{+}-w_{t}^{-} \right)[/math]. The learning interpretation is the same as in the previous two cases.</p style="text-align:>
Strategy based on averaging across rolling windows and losses: let [math] \left(R_{1}\leq R_{2} \leq \dots R_{M}\right)[/math] denote a sequence of rolling windows for obtaining the original sign prediction [math] \widehat{s}_{t|t-1}[/math]. Then, define the average signal obtained from downweighting those rolling windows that have inferior performance during the sequential evaluation of the sign forecast errors [math] sgn\left[\sum_{m=1}^{M}2^{-S_{tj}}sng(\widehat{r}_{t+1|t})\right] [/math], where [math] S_{tj} [/math] is one of the loss functions previously defined, i.e., one of [math] \left(2^{-n_{t}}, 2^{-h_{t}}, 2^{-\nu_{t}}\right)[/math] The learning interpretation is the same as in the previous two cases.</p style="text-align:>
A critical aspect of this approach is the resetting of the counters of the sign forecast errors and the financial loss. Selecting an N that is too large will not work so a more frequent resetting is required and N has to be relatively small, to capture the local behavior of both the series of actual signs and also the local performance of these strategies. Please consult the Python code at my github repository for more information as to how I implement this idea of resetting.
How does this method works in practice? It works well and it works robustly - and you should remember that it is applicable to any signaling strategy that you might have! Below I will illustrate its effectiveness using daily returns for a number of ETFs, starting in 2022. The smallest rolling window is [math] R_{1}=3[/math] while the length of the largest rolling window M and the frequency of resetting N are given in the table that follows. You can easily experiment by changing these parameters, and also changing the rebalancing frequency, by adapting the Python code. Table 1 below holds the results - let's take a look.
Not only learning works but learning with average (a veritable real-time and real-life approach) works as well. The results in the table are very robust, in the sense that both the ex-post optimal rolling window clearly outperforms the passive benchmark but also the averaging works by a rather satisfying margin. And these results are only indicative, I have not performed a full parameter search to optimize them - and you really don't need that too, for there are many parameter combinations that will offer you performance higher than the benchmark. Cross-validation can easily be used to select the parameters, and I would like to stress that the crucial element here is N - for this determines the resetting of the loss functions.
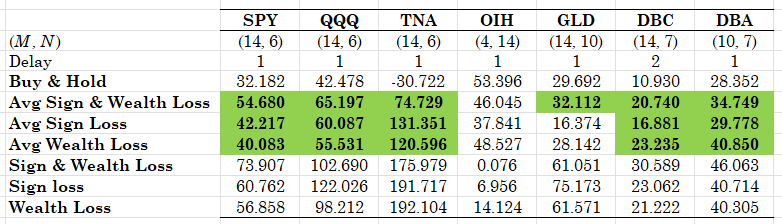
Table 1. Performance of the "speculative learning" strategy, daily rebalancing, results are total returns in percent, data start from 2022-01-1. With green highlighting are the results on the average weighting using the sign and wealth loss functions that outperform the passive benchmark. The results of the last three rows are obtained using the ex-post optimal rolling window.
Figure 1 has a representative plot for TNA, which illustrates the potential of the method using learning by averaging. The difference in performance with the passive benchmark is obvious - grab the Python code and start learning for yourself; and not just learning, speculative learning!
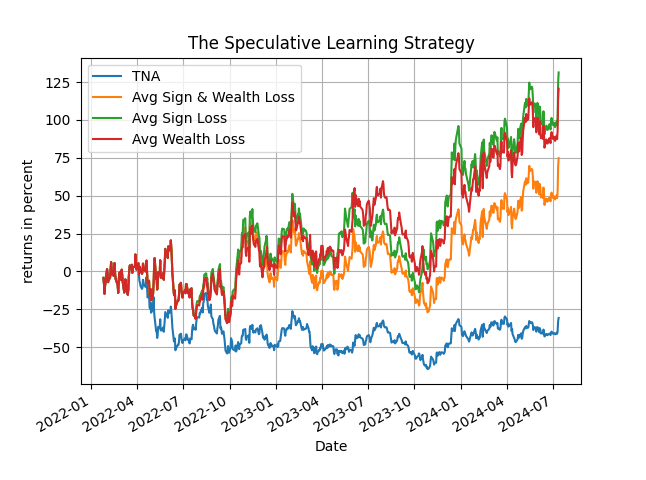
Figure 1. The evolution of total returns for the "speculative learning" strategy for TNA, daily rebalancing, data start from 2022-01-01



