By D. Thomakos
Browsing in JSTOR I chanced to read through a sequence of papers of another pioneer of finance, M.F.M. Osborne, and in particularly this 1959 paper - a significant and defining precursor on Geometric Brownian Motion (GBM) as a model stock prices. Reading through I came to this passage:

We now know well these early results of Osborne, but what gave me the inspiration was the phrase "buy at random and throw it in the box". This relates to properties of the random walk, also explored in a similar context in one of my papers here, that the starting point can be anywhere in a sample realization. Still, for a trading strategy that can be replicated I needed some guidance as to how to apply the results and suggestion in Osborne to advantage - and here is what I came about.
Using equation (25) from above we can immediately obtain that the expected percent change from the current starting point and [math] \tau [/math] periods in the future is given by:
[math] d_{t+\tau} \doteq \left[\mathbb{E}(P_{t+\tau}) - P_{t}\right]/P_{t} = 0.5\sigma^{2}\tau [/math]
where [math] \sigma^{2} [/math] is the variance of the returns. This defines the model-based growth rate over an investment period and it can be compared with the "throw it in the box" return over the same period. Let us define the cumulative returns over that period by [math] c_{t+\tau} \doteq \prod_{j=1}^{\tau}(1+R_{t+j})-1[/math], with [math] R_{t+j}[/math] denoting the period-by-period percent returns, and let us define a measure of "expected excess returns" by [math] x_{t+\tau} \doteq c_{t+\tau} - d_{t+\tau}[/math]. I then define my signal rule as follows:
[math] s_{t+\tau+1|t+\tau} \doteq I(x_{t+\tau} \leq \kappa)-I(x_{t+\tau} > \kappa) [/math]
for some threshold [math] \kappa [/math]. This trading rule essentially suggests that, if the GBM model is appropriate, that we short the market when actual returns exceed, by a margin of [math] \kappa [/math], the expected growth of the underlying asset - which seems like a "bubble", ain't it?!
It's as simple as that. The horizon [math]\tau [/math] becomes our rolling window and the only parameter left to determine is [math] \kappa [/math]. Applying this very simple rule over different rolling windows one can test the assertion of Osborne easily. I use some of our well-known ETFs from previous posts, weekly (from 2000) and daily (from 2022) returns and find some very exciting, and speculatively good, results. The range of the rolling windows is [math] \tau \in \left\{3, 4, \dots, 26\right\}[/math] and I search for some "optimal" value of [math] \kappa [/math] (a crude search, you can easily refine it). Table 1 below has the results, where I present some statistics about the excess returns over the buy & hold benchmark across all rolling windows. Additional details can always be found in the Python code in my github repository.
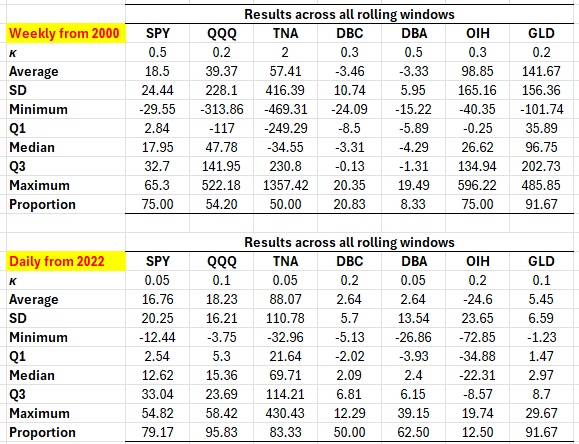
Table 1. Performance attribution of the "Osborne's Bubble" strategy. Weekly and daily rebalancing, data starting in 2000 and 2022 respectively, statistics are across all combinations of rolling windows (τ), delay is always 1-period, the range of rolling windows is 3 to 26 periods, proportion denotes the number of rolling windows that produced excess returns wrt the benchmark. Please consult the Python code for more details.
The results are highly suggestive: for assets where their trend dominates their volatility, such as the equity indices and possibly energy services, the idea works on average very, very well; for the commodity ETFs the results are mixed, with gold showing greater performance in the longer period and the weekly returns. But overall, the idea that you can use our suggested sign forecast appears to be robust and to somehow validate Osborne's observation from 1959. If one can think of a cross-validation approach for the selection of [math]\kappa[/math] then the method is easily applicable in real-time trading. Go then, do your homework and enjoy the speculative profits from "Osborne's Bubble"!



