By D. Thomakos
The summer heat is, at least here in Athens, not much conducive for advanced research - the heat is around 94o F and today being Sunday the beaches around Athens are full! Therefore, as you enjoy the day and you are in the mood for something, well, simple and speculatively cool, here is the "lazy moments" strategy. It cannot be simpler to compute, it works, and you should be able to offer its interpretation too - so read on!
For a rolling window of size [math] R[/math] compute the sample mean [math]\hat{\mu}_{t}(R)[/math] and the sample median [math]\hat{\delta}_{t}(R)[/math], and then construct your signal variable as the ratio of the two:
[math] s_{t-d+1}(R) \doteq \hat{\mu}_{t-d+1}(R)/\hat{\delta}_{t-d+1}(R) [/math]
where [math]d \geq 1[/math] is the delay of the signal. Trading occurs as usual with the formula [math] r_{t+1|t-d+1}^{lazy} \doteq r_{t+1}\cdot sgn\left[s_{t-d+1}(R)\right][/math]. Why and when does this strategy work? This is your homework, for it has a nice theoretical interpretation - when the mean and median do have the same sign (either positive or negative) the signal says to buy the underlying asset, but when they don't the the signal says to sell the asset. You should provide the details of the rest of the explanation in your homework!
Since this method too depends on a rolling window, note that the ex-post optimal selection of it, that I usually showcase, is mostly infeasible in practice. However, there is a simple solution to this predicament - in the current and other strategies - and it is based on wealth rotation: At any time period select the signal that is based on the rolling window that has generated, up to that point, the highest wealth - and you are set for a real-time strategy implementation. As you will see this idea works very well. More details you can find in the Python code in my github repository.
Now for some results, with particular focus on you (the investor!) being truly lazy in the summertime: you do not want to rebalance frequently - say once a week - and you do not want to rebalance with last minute data; you are for a relaxed drive I say! There are results below for a weekly frequency rebalancing and in all but one of them the delay is greater than [math] d \geq 2[/math], which implies more than ample time to compute your signal and place your trade! The usual suspects serve as my data, a bunch of standard and wilder ETFs, and the results appear in the table below - they are from 2018 but you can adapt the code to experiment in any period you want, and also any frequency. Note also that I present parametrizations that are optimal for the real-time implementation of the method.
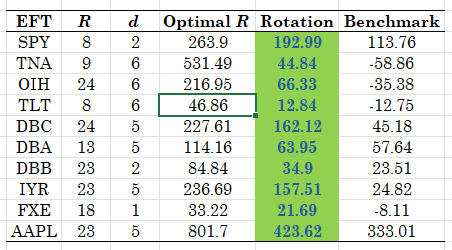
Table 1. Performance of the "lazy moments" strategy, weekly rebalancing, results are total return in percent and are for the best delay parameter d, and the best ex-post optimal window R for that delay - data start in 2018, evaluation starts R weeks after.
There are two results of practical interest in Table 1: (a) both the ex-post optimal approach and the real-time approach work very well; clearly the real-time choice based on rotation will never be as good as the infeasible ex-post optimal strategy but, nevertheless, it is profitable across all ETFs examined; (b) the trading delay can be as small as 1 or 2 (weeks) and as large as 5 or 6. This makes the suggested methodology not just immensely practical but also allows one to update the signal should more information becomes available or should another method is used in conjunction with this one. Be that as it may, what we have here is a strategy that is so easy to compute, and immediately scalable to any number of assets, that you cannot afford not to consider it as part of your quantitative strategies toolbox. You might be lazy during the summer months, but the "lazy moments" is going to be working for your speculative refreshment!
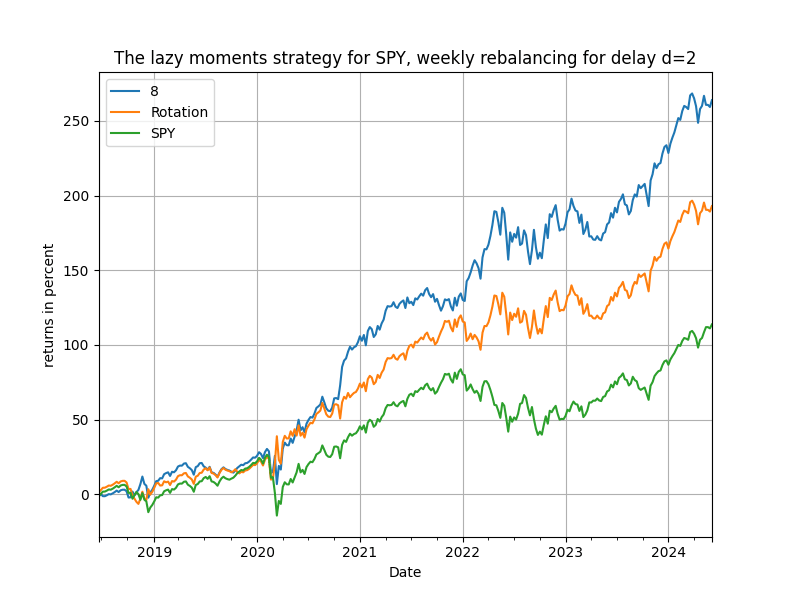
Figure 1. Total cumulative returns for the "lazy moments" strategy for the ex-post optimal rolling window, for wealth rotation and the passive buy & hold benchmark, weekly rebalancing, SPY.
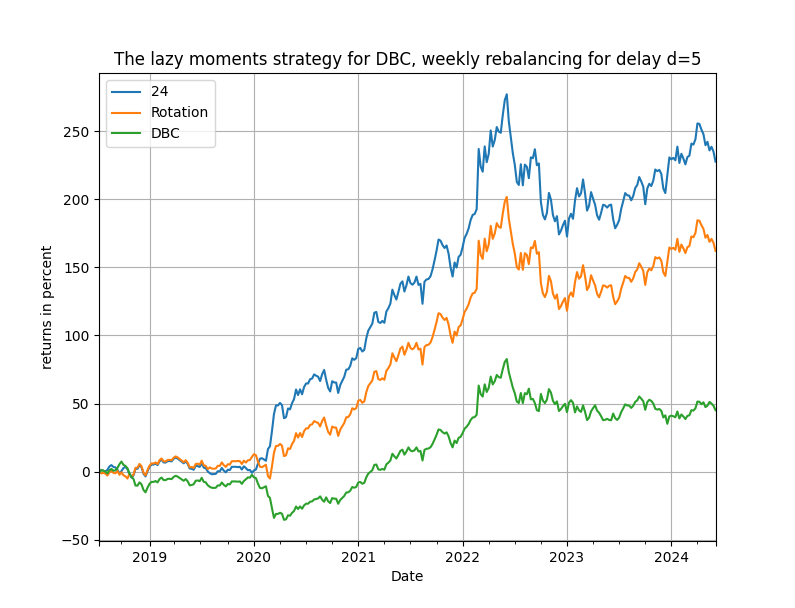
Figure 2. Total cumulative returns for the "lazy moments" strategy for the ex-post optimal rolling window, for wealth rotation and the passive buy & hold benchmark, weekly rebalancing, DBC.



