By D. Thomakos
Athens is home to famous historical places and contemporary tourist attractions; but it is also home to a highly performing stock market that operates along the growth trends of a recovered Greek economy. In this post I explore a number of different trading strategies using daily data kindly provided from the Athens Exchange Group, to which I am grateful for this opportunity. Let's see then what we can find out about the Athenian investor!
First, a few things about the data. They are daily returns from 2019 to 2024, spanning 3 major market indices (composite share price index, or general index, GD; the FTSE large cap index, FTSE; and the FTSE mid cap index, FTSEM), and 9 sectoral indices (banks, BN; technology and telecommunications, TT; financial services, FS; real estate, RE; consumer discretionary, CD; consumer staples, CS; industria,l IN; basic materials, BM; and energy and utilities, EU). Armed with this extensive dataset I proceed to explore three quantitative trading themes: (1) the informational content of sectoral momentum, (2) the construction of a composite sectoral index based on volume, turnover and returns combined, and (3) a regression-based forecast using groups of sectors to predict the market indices.
My analysis is performed for the whole of the sample period and is, importantly, fully implementable in real-time: the signal lag in all methods is 2 days and thus it is immediately computable from the release of historical data. I will next summarize each of the three approaches and illustrate the construction of the corresponding signal variables. To this end, let [math] y_{t}^{i}[/math] denote the daily return of any of the 3 major market indices and let [math] x_{t}^{s}[/math] denote the daily return of any of the 9 sectors. Then, let [math] V_{t}^{s}[/math] denote the daily volume of any of the 9 sectors and correspondingly let [math] T_{t}^{s}[/math] denote the daily turnover and [math] P_{t}[/math] denote the daily closing price of each of the 9 sectors.
The cross-sectional momentum strategy of the sectors is a straightforward application of standard momentum ideas in the literature. If [math]Q_{tp} \equiv Q_{tp}(x_{t}^{1},x_{t}^{2},\dots,x_{t}^{9})[/math] math denotes the pth cross-sectional quantile of the daily sectoral returns, then I construct my momentum signal variable as follows:
[math] s_{t}^{mom} \doteq sgn(Q_{t-2,0.75}) - sgn(Q_{t,0.25})[/math]
and the trading returns are given by [math] r_{t+1|t}^{i,mom} \doteq y_{t+1}^{i}\cdot s_{t}^{mom}[/math], for each index i. This is a variation of "buy the winners and sell the loosers" strategy but different: instead of explicitly identifying to which sectors to invest I look for the signs of the quartiles of the cross-sectional distribution and use those to trade the index returns. This is a very interpretable strategy and of immediate implementation, as it has no parameters to estimate or calibrate (one can of course consider different values for the quantiles - try this on your own!)
The composite sectoral index strategy has a few steps in its construction. First, I scale the volume, turnover and price series by their initial value to make them comparable, i.e., I define [math] v_{t}^{s} \doteq V_{t}^{s}/V_{0}^{s}[/math] and similarly for [math] \tau_{t}^{s}[/math] for turnover and [math]p_{t}^{s}[/math] for prices. After scaling I compute the cross-sectional means as in [math]\bar{v}_{t} \doteq \sum_{s=1}^{9}v_{t}^{s}/9[/math] and similarly for [math]\bar{\tau}_{t}[/math] and [math]\bar{p}_{t}[/math]. Then, I define my sectoral index variable as [math]SI_{t} \doteq \bar{v}_{t}/\bar{\tau}_{t} - \bar{p}_{t}[/math] and take a non-linear transformation of its daily percent change as in [math] si_{t} \doteq tanh\left(\Delta SI_{t}/SI_{t-1}\right) [/math]. Then, I compute the 14-day rolling, time-series 90% quantile of this index as in [math]Q_{t,0.9}(si_{t-R+1}:si_{t})[/math] with R=14 days. Finally, I compute the second signal variable as in:
[math] s_{t}^{SI} \doteq I(si_{t-2} \leq Q_{t-2,0.9}) - I(si_{t-2} > Q_{t,0.9}) [/math]
with corresponding trading returns are then given by [math] r_{t+1|t}^{SI} \doteq y_{t+1}^{i}\cdot s_{t}^{i, SI}[/math]. This completes the description of the first two trading approaches. Note, again, that we are using only sectoral information to predict the 3 major market indices.
Now, for the final strategy that relies on factor regression with model reduction. I first split the 9 sectoral returns into three groups as follows: the first factor group comprises from the consumer staples, the industrials , the basic materials and energy and utilities [math] \mathbf{f}_{t}^{1} \doteq \left[x_{t}^{CS}, x_{t}^{IN}, x_{t}^{BM}, x_{t}^{EU}\right]^{\top} [/math]. Similarly, the second factor group comprises from banks, technology and telecommunications, financial services and consumer discretionary [math] \mathbf{f}_{t}^{2} \doteq \left[x_{t}^{BN}, x_{t}^{TT}, x_{t}^{FS}, x_{t}^{CD}\right]^{\top} [/math], and the third factor is real estate alone [math]f_{t}^{3} \doteq x_{t}^{RE}[/math]. The split can be justified, and I will do so momentarily, but of course you are free to make your own variable choices! Now, the three groups reflect sectors of more fundamental or "traditional" goods and services vs sectors of more innovative and contemporary ones. Furthermore, the post-crisis real estate boom (mainly in private property ownership transfers) suggests that we use the real estate sector on its own. The encompassing model is thus written as:
[math] y_{t}^{i, 123} = b_{0} + \mathbf{f}_{t-2}^{1,\top}\mathbf{b}_{1} + \mathbf{f}_{t-2}^{2,\top}\mathbf{b}_{2} + f_{t-2}^{3}b_{3} + u_{t}[/math]
and I consider all component models of factor groups [math] g = 1, 2, 3, 12, 13, 23, 123[/math]. For each model I use a rolling window of R = 14 days for parameter estimation and perform two rounds of sequential model reduction; after that the forecast is computed with corresponding trading returns being given by [math] r_{t+1|t}^{i,g} \doteq y_{t+1}^{i}\cdot \widehat{y}_{t+1|t}^{i,g}[/math].
Armed with these three trading approaches we can now see some representative results on total trading returns plus some interesting plots - since the data are proprietary and I cannot give them out please ask for the corresponding Python file if you can have access to the data. Table 1 has the summary of trading results for all three approaches and their corresponding combinations where available.
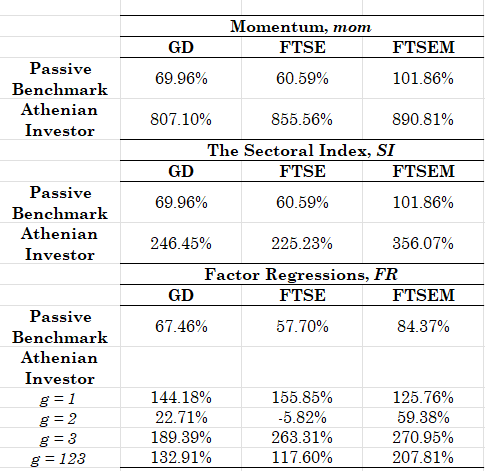
Table 1. Performance of trading strategies for the momentum, composite sectoral index and factor regressions, daily returns, estimation where required by a 14-day window, data start from 2019 - the strategies are applied to the general index GD, the FTSE large cap index and the FTSEM mid cap index.
The results require no, or little, discussion. It is very clear that that sectoral performance is a driver of market performance, and that there exist at least the strategies presented above that can lead to trading profitability. Naturally, there is information in the momentum structure or the composite index that one can take advantage of via some other approach - but the critical thing is that the information is embedded within the sectors. Furthermore, it is immediately clear from the third panel of the table that it is the real estate sector that acts as a performance driver in the factor regressions approach, an interpretable result given the state of the Greek economy over the period of evaluation. All three approaches allow for massive excess returns over their corresponding passive benchmarks, and this holds for different sub-periods as well (with some changes in the parametrizations) - but this is something for your homework to discover!
While you browse below on some nice plots on trading performance from the table, I only wonder whether Socrates or Plato, at least Pericles, would have been representative of the Athenian investor!

Figure 1. Total cumulative returns of the general index GD and the sectoral momentum strategy

Figure 2. Total cumulative returns of the general index GD and the sectoral index strategy

Figure 3. Total cumulative returns of the general index GD and the sectoral factor regressions strategy (note the response of the full factor model druing the 2020 Covid-19 crisis)



