By D. Thomakos
In this post I further explore the ideas behind updating and learning probabilities for quantitative trading strategies. I introduce two new rules for probabilistic forecasting for trading, based on the speculative differential, the probability difference between a long and a short position. The first rule is an extension of my own work on adaptive learning in continuous variables in a probabilistic context; the second rule is modification of said adaptive learning geared directly towards the estimation of the speculative differential. Both rules work very well and are highly recommended, based on the limited testing presented below. It is crucial, however, to understand the context into which they operate, and this is what we are going to start with.
Consider the speculative differential defined as [math] \mathbb{D}(r_{t+1}) \doteq \mathbb{P}(r_{t+1} > 0) - \mathbb{P}(r_{t+1} \leq 0) \equiv 1 - 2\mathbb{P}(r_{t+1} \leq 0) [/math]. When implementing any quantitative trading strategy, this differential determines the direction of your future returns and the accuracy of your trading position. It is thus instructive to attempt to forecast this differential by estimating the corresponding probability of a short position and, furthermore, to consider the composite rule that will attempt to trade based on the product of the sign of the expected returns themselves times the speculative differential - that is the product of [math] \mathbb{E}(r_{t+1})\cdot \mathbb{D}(r_{t+1}) [/math]. For predicting the expected returns, one could use any method from my previous posts - and the same could be done for the probabilities, see for example here and here. Let me now extend probabilistic learning and forecasting with two rules that can easily be implemented to any quantitative trading toolbox. As always computational and implementation details can be found in my github repository.
The first rule is a direct implementation of adaptive learning, see the reference above, into probabilities and is written as:
[math] p_{t+1|t}^{adt} \doteq p_{t+1|t}^{avg} + \gamma e_{t|t-1}^{adt}[/math]
where [math] p_{t+1|t}^{avg}[/math] denote any input forecast for the probability of negative returns; here I simply use sample (recursive or rolling) proportions on the variable [math] y_{t} \doteq I(r_{t} \leq 0)[/math]. The pair [math] (p_{t+1|t}^{adt}, e_{t|t-1}^{adt}) [/math] denotes the probability forecast and corresponding forecast error for adaptive learning. The learning parameter [math] \gamma [/math] is estimated by a simple application of a least-squares like procedure (note that this is quite different from the estimation of the learning parameter in the original paper). Look for details in the code!
The second rule is based on a different idea which starts as a modification of adaptive learning. Consider now the updating rule:
[math] p_{t+1|t}^{ada} \doteq w(\alpha) p_{t+1|t}^{avg} + \left[1-w(\alpha)\right]e_{t|t-1}^{2,ada}[/math]
which is ad-hoc of course but has its natural interpretation of interpolating between an input forecast and the (squared) forecast error. The trick here is in the definition of the weights. If the weights are obtained as the (scaled to sum to one) versions of the following initial rule [math] p_{t+1|t}^{ada} \doteq \alpha^{2} p_{t+1|t}^{avg} + (1-\alpha)^{2}e_{t|t-1}^{2,ada}[/math], then one can find the value of [math] \alpha [/math] that minimizes [math] \mathbb{D}(r_{t+1}) [/math] period-by-period. This minimization implies selecting a weight to assign maximum probability into sorting the underlying asset and it can be interpreted as an attempt of accurate sorting. Once the "optimal" value of [math]\alpha^{*}[/math] is computed then the weights are easily obtained as [math] w(\alpha^{*}) \doteq \alpha^{*}/(2\alpha^{*} - 2\alpha^{*} + 1) [/math] and then the probability can be updated.
There are 7 trading rules that can now be applied, for either a recursive window or a rolling window of R observations: (1) based on the sign of the sample mean of the returns, which forecasts expected returns; (2) based on the speculative differential when estimated by sample proportions; (3) based on the speculative differential when estimated by the adaptive learning rule adt; (4) based on the speculative differential when estimated by the adaptive learning rule ada; and rules (5), (6) and (7) that use the product of (1) with (2), (3) and (4). Since I use both a rolling and a recursive estimation approach I have a total of 14 different trading rules.
For the empirical implementation I consider weekly returns from 2011 and rolling windows in the range of 3 to 26 weeks, that is a total of 24 rolling windows. Thus, my evaluation is on a grid of 14[math]\times[/math24 = 336 combinations of trading rules and rolling and recursive windows. I consider a bunch of standard ETFs for the evaluation: SPY, QQQ, GLD, DBC, DBA, DBB, GLD, OIH, TNA plus the Bitcoin and the Ethereum, and I report the top-3 performing trading rules plus some statistics on the percentage of trading rules among the 336 combinations that generated excess returns over these assets. The results are summarized in Table 1.
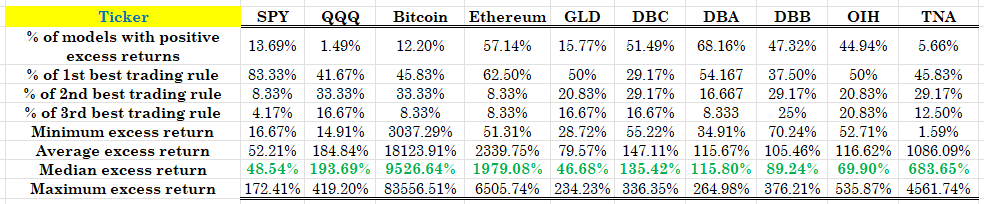
Table 1. Performance attribution of the speculative differential strategy. Weekly rebalancing, data starting in 2011, statistics are across all combinations of rolling windows and trading rules.
The results are suggestive of the practicality and profitability of these trading rules. With the exception of the QQQ and TNA ETFs, all other assets have a large percentage of models (combinations of rolling windows and trading rules) that generate positive excess returns and the median excess return across all such combinations of successful trades are large enough to guarantee at least a consideration for these rules (if not their direct implementation). The results on the commodity ETFs are particularly encouraging as are the results on the two cryptocurrencies. If you run the code, you can easily access which trading rules appear mostly as the top-3 performing ones (and you should, do your homework!) These results, being aggregated across methods and rolling windows, avoid the forward-looking bias that is inherent in all such exercises that we conduct in Prognostikon and you should consider them as quite strong. It's up to you to adapt the code to your choices and make sure that you don't miss out but do use the speculative differential - plus there is more coming your way on this front of trading with probabilities, so stay tuned!



