By D. Thomakos
This is going to be a rather short post, think about it as a "sweet" follow-through to my last post on currency and money market funds as unemployment proxies. Inflation and unemployment are related, or so the macro people say, and therefore it was only natural to look after the potential forecasting ability of some similar monetary variables with respect to inflation. Read through and grab the code in my github repository for your own experimentations!
Take two money demand variables at the monthly frequency, the currency in circulation component of M1, as in the previous post, and the demand deposits and form their ratio, and then take the y-o-y percent change of it; call this your [math] x_{t} [/math] variable. Then, take the monthly CPI-based (annual) inflation and call this your [math] y_{t} [/math] variable. The question being asked is this: does the explanatory variable of currency over demand deposits lead inflation and if so by how many months? The idea is extremely simple: currency and demand deposits are money demand variables but with different liquidity and for different purposes: if their ratio increases then people are using more of their immediate liquidity and possibly depleting their savings; they do not worry about future price increases and prices should, probably and on average fall. If, on the other hand, this ratio decreases then people are removing immediate liquidity from the market for saving for a future date, and this substitution possibly signals future price increases. Be that as it may, what I do is standard fair: I compute the cross-correlation between current inflation and the lagged currency-to-deposits ratio and look for some degree of causality (I do this starting from 2017, you can experiment with the robustness of results from different dates). Thus, computing [math] \hat{\rho}(y_{t},x_{t-d})[/math] for various values of the delay parameter d I get Figure 1 below. As you can see at around 12-13 months this cross-correlation hits at over 90%. Makes sense then to use it in the context of a forecasting regression.
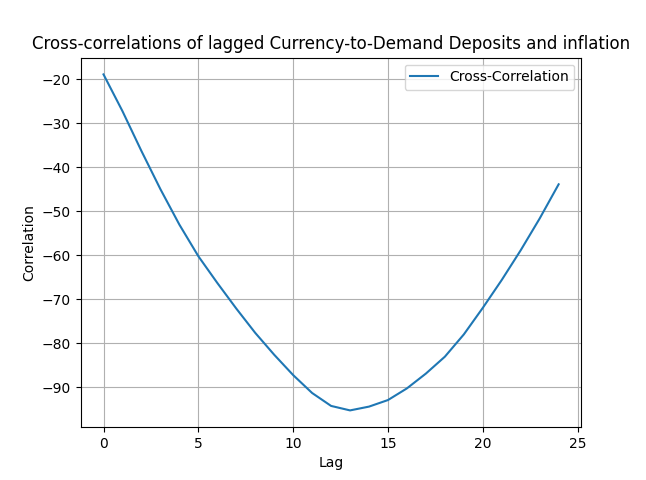
Figure 1. Cross-correlation between lagged the currency-to-demand deposits ratio and inflation.
I estimate a simple delay regression of the form [math] y_{t} = \alpha + \beta x_{t-d} + \epsilon_{t}[/math] with the delay determined by the results in Figure 1 and immediately obtain the long-term (year-ahead) inflation forecast as [math] \hat{y}_{t+d} = \hat{\alpha} + \hat{\beta}x_{t} [/math], which is plotted in Figure 2. In the code you have the option to add a dynamic component to the forecast (which slightly increases the forecasted inflation values).
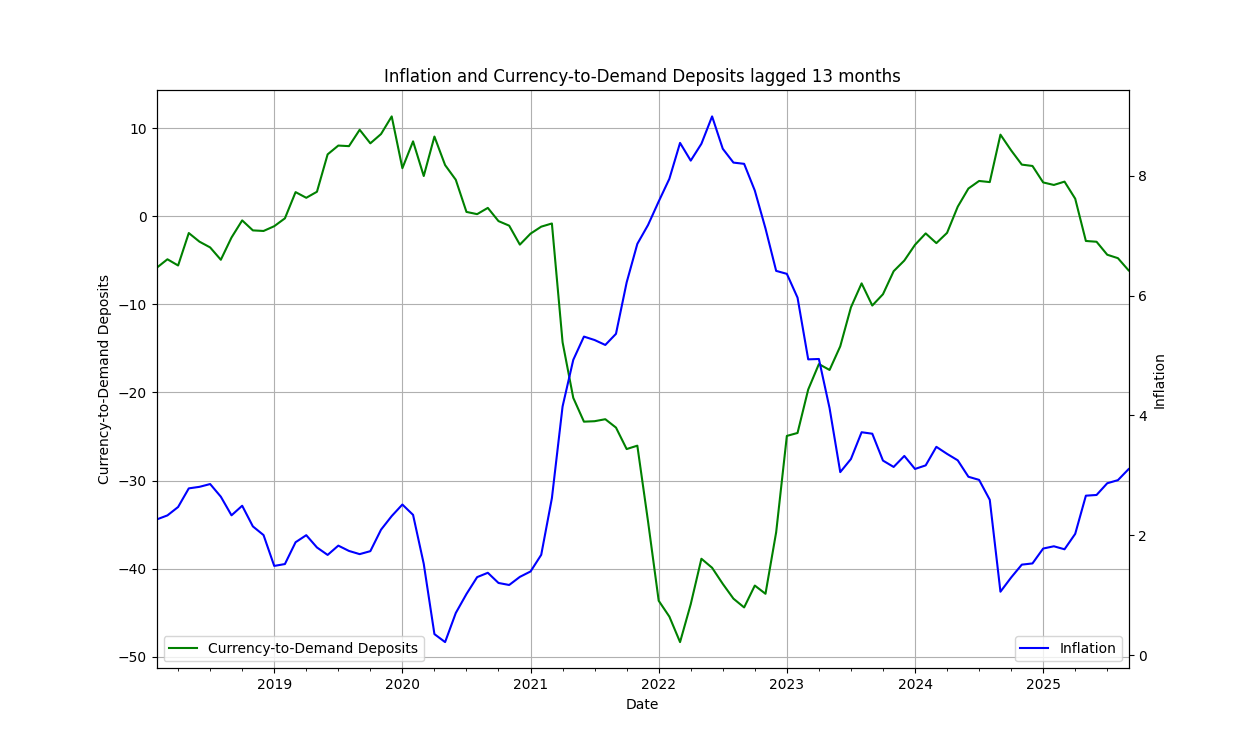
Figure 2. The lagged currency-to-demand deposits ratio and a year-ahead inflation forecast.
You can see the mirror image of the two variables and the rising inflation, a natural model-by product given the inverse relationship of the two variables. That was easy right? You can add on top of this kind of modeling all sorts of more complicated model and ideas, true. But this serves as a good benchmark and a stark reminder that complexity and complicated models are not always necessary for understanding causality in time series forecasting and econometrics (but then again comments welcomed!) Grab the Python code and experiment yourselves, who knows...maybe there is a secret here for trading as well!
Many thanks to Giorgio Borelli for pointing out to me earlier work by Simon White of the Macroscope column in Bloomberg. Unfortunately I do not have full access to read the pieces so anyone interested and with access can easily locate them!



