By Panos Xidonas
There’s no doubt that little attention has been paid to the necessity of a principal business context, in which the members of an investment committee decide for the optimal synthesis of portfolios, considering several and conflicting investment criteria. The underlying gap widens significantly, considering that mainstream portfolio theory fails to accommodate, both additional investment objectives, beyond expected return and variance, and analysts’ forecasts, when these are coming in the form of discrete recommendations. This post is a summary of a recent publication titled "Grouped data, investment committees & multicriteria portfolio selection", appearing in the Journal of Business Research. The use of humans as wise decision makers, when combined with the wealth of data available to form financial portfolios, is what makes the link of the ideas presented in the paper with the judgmental forecasting literature.
The central contribution of one of our recent papers (Xidonas et al., 2021) is associated with the introduction and standardization of a unified decision support business framework, which deals with all the above complexities and facilitates asset managers in their professional practice. As Elton & Gruber (1987) argue, almost all of the literature in finance analyzing the selection of optimum portfolios assumes that the agent making the decision has a full set of estimates of the expected return for each security and the variance-covariance matrix between securities. However, in actual practice most practitioners simply receive a list of stocks with a ranking on each stock (usually from 1 to 5) and perhaps some partial risk information: if stocks are grouped from 1 to 5, then stocks ranked in group 1 are best buys, while stocks ranked 5 are definite sells. Thus, the practical utilization of grouped data is a critical issue. Since these are the inputs most investors exploit to make investments, the adjustment of classical portfolio theory is necessary in order to secure the optimality of the underlying decisions.
The previously mentioned codings make up the information communicated to an investment committee. However, according to Mottola & Utkus (2009) “the decisions investment committees make, often overshadow an important fact; groups, by their nature, make decisions that are susceptible to behavioral and psychological biases. And these biases may generate irrational decisions, which can influence portfolios’ returns and augment exposure to fiduciary risk”.
Our purpose in Xidonas et al. (2021) was to develop an integrated multicriteria portfolio selection methodology for group decision support, combining the business practice of grouped data with the classical theory of portfolio analysis; moreover, the value of the suggested framework is enriched with the introduction of a novel concept in the field of investment decision making for groups, i.e., the ‘signal-consensus impact plane’, a data analytics tool which provides effective visualization for the decision makers. The suggested framework fundamentally recognizes that the typical portfolio selection decision process is associated with five (5) problem dimensions and an equal number of solution components:
a) Grouped data,
b) Investment committees,
c) Investment objectives,
d) Portfolio theory, and
e) Approved lists.
Each one is confronted with a specific modeling tool from the field of operations research and decision sciences (Figure 1). The underlying platform, a fully tractable routine, is also adequately compatible with the current normative trends in the whole spectrum of investment management processes, towards highly controlled operations, consistent with the notion of compliance in capital markets.
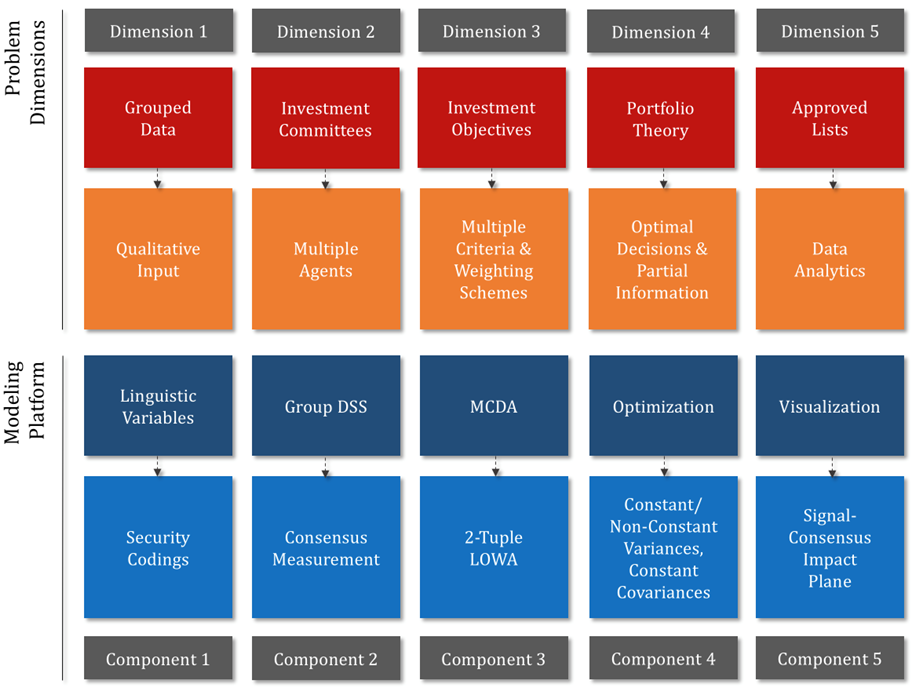
Figure 1. Problem dimensions & modeling platform
The first dimension is associated with the business practice of grouped data, i.e., the utilization of discrete recommendations for characterizing the prospect of each security. Undoubtedly, the fact of directly feeding the proposed portfolio selection methodology with forecasts from analysts (instead of using historical time-series data), provides the suggested process with a highly applicable value, which allows practitioners for exploiting an intuitional and user-friendly investment decision support tool. Linguistic variables are also highly interconnected with the major issue of integrating multiple investment criteria and multiple decision makers, i.e., the second and third problem dimensions,, in the real-world portfolio management practice. Multiple investment criteria, such as return, volatility, liquidity etc. are always under necessary consideration when dealing with actual asset management decisions, while at the same time the demanding task of precise consensus measurement for group decision making, is of crucial significance. The suggested framework utilizes a double exploitation of the 2-tuple LOWA method (Herrera & Martinez, 2000), both for the initial multicriteria evaluation of the individual assessments of each decision maker and the final overall evaluation, where the decision makers possess the role of the decision criteria. The fourth dimension is connected with the adjustment of classical portfolio theory to the singularity of grouped data with partial information, in order to secure the optimality of the underlying decisions. The adopted strategy is the one of Elton & Gruber (1987) and two (2) types of optimal portfolios are constructed, i.e., investment baskets complied with the assumption of: a) either constant variances and constant covariances, or b) non-constant variances and constant covariances. Finally, the fifth dimension of the problem and corresponding contribution of the suggested decision framework, is associated with the introduction of a novel concept in the field of investment decision making for groups, i.e., the ‘signal-consensus impact plane’, a data analytics tool which provides effective visualization of the approved lists for the decision makers. This plane actually illustrates the extremely important trade-off between the consensus among the decision makers and the overall discrete recommendation for the potential of each security. The various ways that the underlying map can be interpreted are presented in Figures 2a-2b. Also, the process flowchart of the proposed methodology is presented in Figure 3.
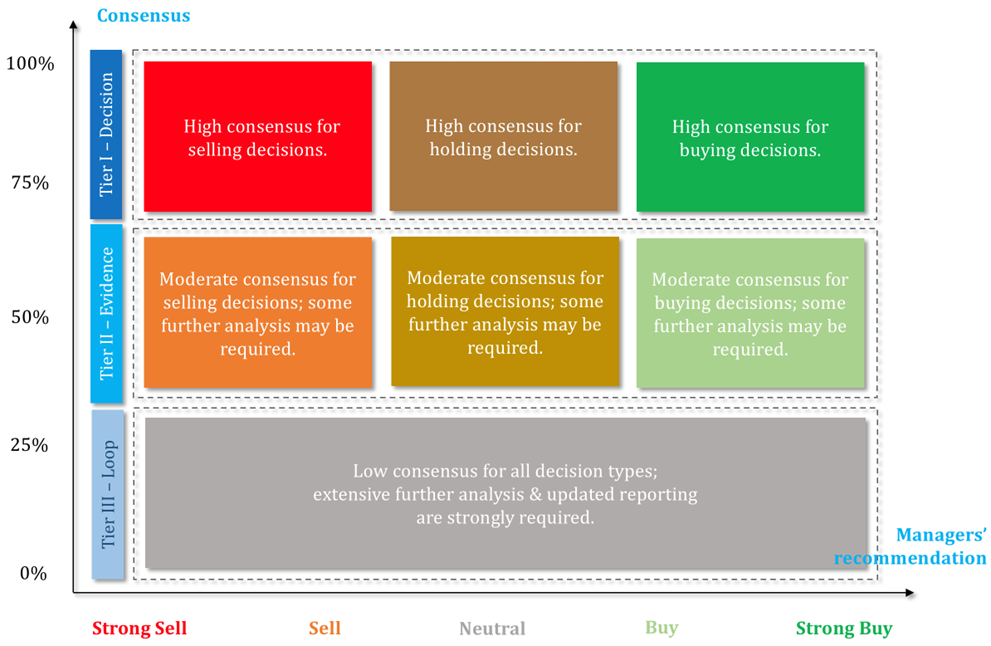
Figure 2a. Theoretical establishment of the ‘signal-consensus impact plane’
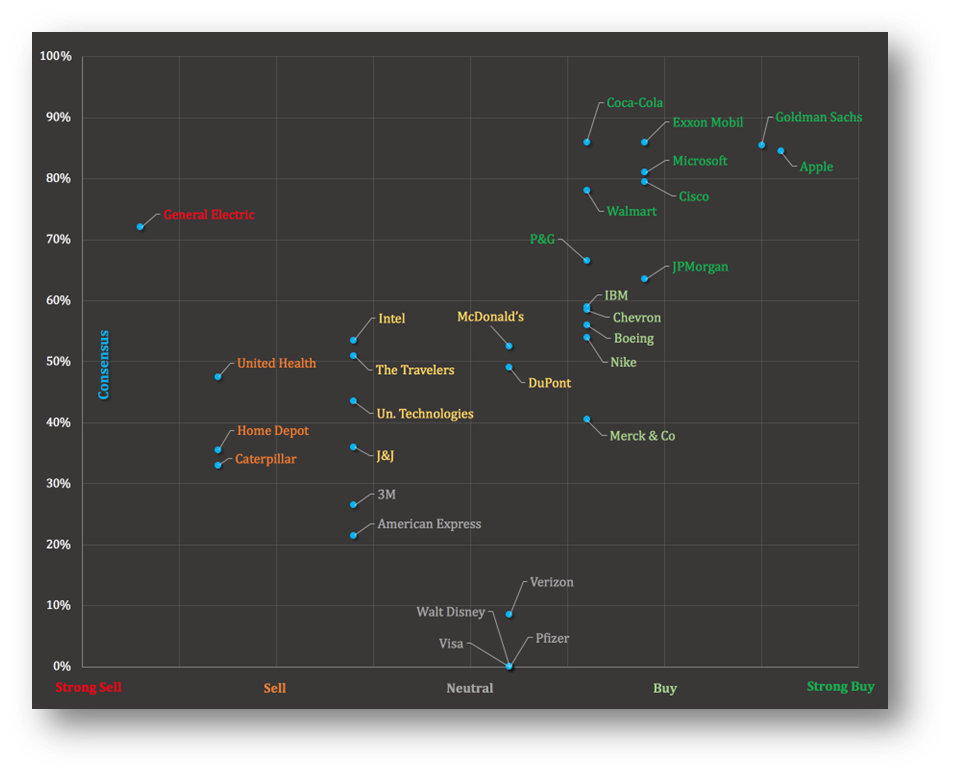
Figure 2b. Theoretical establishment of the ‘signal-consensus impact plane’’
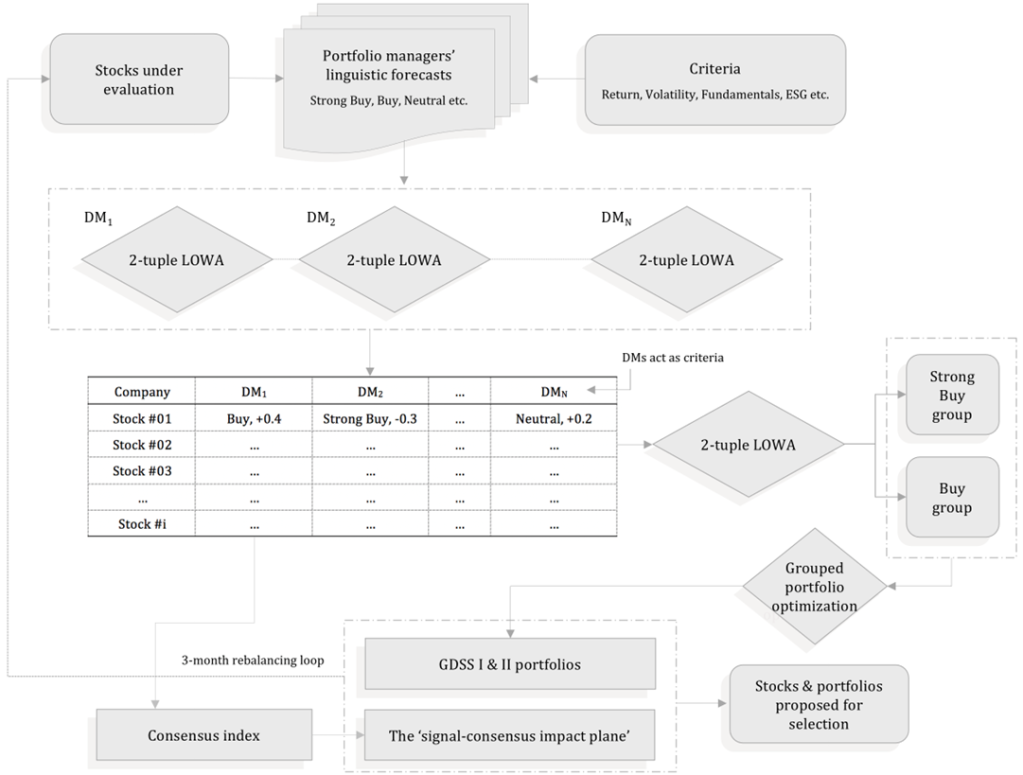
Figure 3. The process flowchart of the proposed methodology
Those readers interested in the excellent performance of the presented approach can read the full paper given at the beginning of the post and may contact the author for additional information.
References
Elton, E., Gruber, M., 1987. Portfolio analysis with partial information: The case of grouped data. Management Science, 33 (10), 1238-1246.
Herrera, F., Martinez, L., 2000. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Transactions on Fuzzy Systems, 8 (6), 746-752.
Mottola, G., Utkus, S., 2009. Group decision-making: Implications for investment committees. Valley Forge: The Vanguard Group.
Xidonas, P., Doukas, H., Hassapis, C., 2021. Grouped data, investment committees and multicriteria portfolio selection. Journal of Business Research, 129, 205-222